推 Salmon415 : 正二報酬只有1.4倍的相關的說法看過很多次了,第一 11/26 03:53
→ Salmon415 : 次看到有解釋這麼清楚的文章,感恩大大,股板清流.. 11/26 03:53
推 fuhoho : 推分析 11/26 03:55
推 xinWu : 認真分析推 11/26 03:59
推 chisheng74 : 推 11/26 04:22
推 namkk : 對數常態分配 推一個 11/26 04:48
推 flyawayla : 推 11/26 04:48
推 cleanx : 真的在寫論文 11/26 05:05
推 forsenbaj : 這篇文章值得被收進精華區 11/26 05:09
推 freepure : 感謝用心分享 11/26 05:41
推 m840509 : 用期貨就半年平衡一次 11/26 05:45
推 lanewyoung : 推 11/26 05:58
推 namkk : 你說大仁哥的再平衡策略最後跟原型一樣 教徒們情何 11/26 06:03
→ namkk : 以堪 11/26 06:03
推 nickelpig : 謝謝您的分享! 11/26 06:03
推 kevinchuang : 打破正二1.4倍報酬 還是比較高的迷思 11/26 06:04
→ kevinchuang : 也肯定大仁哥 ,正二比起其他奇奇怪怪的金融(騙錢 11/26 06:05
→ kevinchuang : )相比已經至少是正常的投資工具 11/26 06:05
推 budaixi : 沒這篇文很多人還活在自己認知吧 11/26 06:16
推 snahwwww : 該推~ 11/26 06:23
推 herculus6502: 推 11/26 06:28
推 FreeWretch : 好 11/26 06:34
→ FreeWretch : 不知能不能看到大仁哥一起來討論 11/26 06:35
→ linjunyou : 以台灣市場來說,回測報酬率結果正二是原型快3倍, 11/26 06:35
→ linjunyou : 該如何解釋? 11/26 06:35
→ sheenscott : 回樓上,不解釋,因為那只是其中一條路徑 11/26 06:41
→ sheenscott : 其他時間段、不同國家、不同指數,都會得到不同結 11/26 06:41
→ sheenscott : 果,會問這個問題,就表示蒙地卡羅那邊沒有看懂 11/26 06:41
推 shorty696820: 太優質了 11/26 06:41
推 namkk : 原PO您好 讓我無知地問一下 11/26 06:48
→ namkk : -- 11/26 06:48
→ namkk : 這「3萬條路徑」中,有一半的路徑走完之後,你的實 11/26 06:48
→ namkk : 際報酬只有原型的1.4倍 11/26 06:48
→ namkk : -- 11/26 06:48
→ namkk : 其他一半的路徑 去哪裡了?? 謝謝 11/26 06:48
推 spike1215 : 正二本身就自帶再平衡了,再外掛一層再平衡真的很 11/26 06:53
→ spike1215 : 不能理解 11/26 06:53
推 IanLi : 推認真文,另外以過去資料分析,問題就是未來是否 11/26 06:56
→ IanLi : 有再現性,若認同指數投資,簡單點更容易長久去實 11/26 06:56
→ IanLi : 踐。 11/26 06:56
→ sheenscott : 回樓上,我剛剛回去看了一下,那邊的描述確實不是 11/26 06:57
→ sheenscott : 很恰當,果然是半夜寫文太放鬆了(ry 11/26 06:57
→ sheenscott : 比較正確的說法,應該是「其中一半的路徑走完之後 11/26 06:57
→ sheenscott : ,年化報酬『可能』高於100%原型的1.4倍」 11/26 06:57
→ sheenscott : 這邊用可能,是因為原論文沒有給出完整的蒙地卡羅 11/26 06:57
→ sheenscott : 結果,我不清楚LETF組贏過的時候的分佈 11/26 06:57
→ linjunyou : 不同國家、市場、指數會得到不同結果,既然台灣市 11/26 06:58
→ linjunyou : 場是約3倍報酬那條路徑,那不就在台股買正二優勢很 11/26 06:58
→ linjunyou : 大 11/26 06:58
推 dreamdds : 這篇強 11/26 06:58
→ opm : 有的高 有的低吧 真實世界的財富分配 11/26 07:00
→ sheenscott : 回spike大,兩個的再平衡是不同的意義 11/26 07:00
→ sheenscott : 正二本身的再平衡是對單個部位的槓桿率再平衡,這 11/26 07:00
→ sheenscott : 點就算你拿期貨或是融資開槓桿都要面對的,除非你 11/26 07:00
→ sheenscott : 不知道自己在幹嘛,放著槓桿率在那邊亂甩 11/26 07:00
→ sheenscott : 至於像是50/50的那種「再平衡」,指的是對「整體資 11/26 07:00
→ sheenscott : 產」個部位配比的再平衡,這個才是有機會收割到波 11/26 07:00
→ sheenscott : 動率,或至少降低風險用的 11/26 07:00
→ sheenscott : 本質上就跟ETF在追蹤指數的時候,會去做的權重調整 11/26 07:00
→ sheenscott : 一樣,看的是「一籃子資產」的比例 11/26 07:00
噓 afflic : 1. 你拿比較保守的中位數去複利,最後當然會差很多 11/26 07:02
→ afflic : 2. 因為波動大,所以保留現金低點加碼很重要 11/26 07:02
→ sheenscott : 再回lin大,你還是誤會本質上的差異了,台股過去那 11/26 07:03
→ sheenscott : 條路可能走出了好的那條世界線,但是未來?沒人能 11/26 07:03
→ sheenscott : 保證。至少從全世界角度來看,all-in LETF能夠顯著 11/26 07:03
→ sheenscott : 贏原型的市場,反而才是異常存在 11/26 07:03
→ sheenscott : 然後其實通過調整槓桿配比,你是能夠做到不用all-i 11/26 07:03
→ sheenscott : n正2,也能達到跟all-in接近的報酬率的,不過這個 11/26 07:03
→ sheenscott : 有機會再寫一篇分析吧 11/26 07:03
推 willyabs : 感謝分析 11/26 07:05
推 seanflower : 再平衡用報酬率去決定啊 11/26 07:06
→ afflic : 大仁哥原文,給想參考的人比較一下 11/26 07:06
推 askaa : 請訂閱 按讚 打開洨鈴鐺 說得很不錯 推一個 11/26 07:09
→ askaa : 知道跟做得到真的是完全獨立的兩件事情 11/26 07:10
→ sheenscott : 回樓上,那個upper CL的意思是95%信賴區間的上緣的 11/26 07:10
→ sheenscott : 意思,是給你看範圍的上限 11/26 07:10
→ sheenscott : 直接用極端值來當常態評估,就跟拿買樂透一定會中 11/26 07:10
→ sheenscott : 頭獎一樣不切實際,統計學不是這樣用的,望周知 11/26 07:10
→ askaa : 跟你策略完不完整真的幾乎一點關係都沒有 11/26 07:10
→ askaa : 最好的方式 就是心 認知 跟策略 等三角形一樣強 11/26 07:11
→ askaa : 這樣投資 就幾乎不會有大問題了 11/26 07:11
→ sheenscott : 而且在已知LETF的報酬分布,是明顯正偏的情況下, 11/26 07:15
→ sheenscott : 你更有機會碰到的是左尾不是右尾 11/26 07:15
→ sheenscott : 這也是我什麼我特別強調,設定總體資產槓桿率再平 11/26 07:15
→ sheenscott : 衡的原因,能用策略降低風險達到相似水準的平均報 11/26 07:15
→ sheenscott : 酬的時候,沒必要去賭一個中彩券的路徑,但是大多 11/26 07:15
→ sheenscott : 數時候可能輸的更慘 11/26 07:15
噓 afflic : 很多人拿課本上的夏普比率來評估標的好不好 11/26 07:19
→ afflic : 其實有個很大的問題 11/26 07:19
→ afflic : 如果你是一個能夠承擔風險的人,波動大其實是好事 11/26 07:19
→ afflic : 這樣才有低點可以加碼 11/26 07:19
→ afflic : 反之如果你是個不能承擔風險的人,請去買定存 11/26 07:19
→ afflic : 重點是這個標的能不能長期向上,而不是夏普比率高不 11/26 07:19
→ afflic : 高 11/26 07:19
→ afflic : 一堆夏普比率高的標的 11/26 07:19
→ afflic : 都是報酬率不怎麼樣但標準差超級小 11/26 07:19
→ afflic : 這種標的真的能讓你賺大錢嗎? 11/26 07:19
→ sheenscott : 夏普比率拿來分析LETF的報酬確實不是很恰當的一個 11/26 07:25
→ sheenscott : 參數,尤其當你跟其他類型的槓桿組合比較的時候, 11/26 07:25
→ sheenscott : 他們的標準差算出來可能是接近的,會導致夏普率接 11/26 07:25
→ sheenscott : 近 11/26 07:25
→ sheenscott : 實際上標準差跟均值是二階跟一階動差,LETF由於路 11/26 07:25
→ sheenscott : 徑依賴的問題,其實要看的是高階動差,偏態甚至是 11/26 07:25
→ sheenscott : 峰態,因為同樣的標準差但是走的路不同,結果會完 11/26 07:25
→ sheenscott : 全不一樣 11/26 07:25
→ sheenscott : 學界我有看到幾篇論文在探討怎麼更好評估LETF策略 11/26 07:25
→ sheenscott : 的參數,有機會可以另外再來討論 11/26 07:25
→ afflic : 不應該說夏普比率,應該說拿報酬跟風險比較 11/26 07:26
→ afflic : 說夏普比率只是一般人比較常用的方法 11/26 07:26
→ afflic : 現實世界是,很多會讓你賺大錢的標的,風險都超級大 11/26 07:26
→ afflic : 如果因為風險跟報酬不匹配就不投資 11/26 07:28
→ afflic : 那可能就會錯過很多賺大錢的機會 11/26 07:28
→ afflic : 補充一下,這裡的風險指的是股價波動程度 11/26 07:28
推 t0333120 : 感謝解惑數學模型,知道模型的短板在哪裡,就能夠用 11/26 07:29
→ t0333120 : 策略應對,畢竟三萬條路徑中也是有超出水準的表現啊 11/26 07:29
推 Gipmydanger : 你年輕的時候不敢承受風險(其實只是波動更大),就 11/26 07:30
→ Gipmydanger : 是你最大的風險。而且學術定義上的風險(波動)根本 11/26 07:30
→ Gipmydanger : 就不是一般人認知的風險。 11/26 07:30
→ afflic : 其實只要能找到長期向上的標的 11/26 07:31
→ afflic : 不論有幾條路徑低於平均水準 11/26 07:31
→ afflic : 低檔布局都能走向超出平均水準的路徑 11/26 07:31
→ afflic : 理論跟實務的差別在 11/26 07:32
→ afflic : 理論派很怕風險,但實務派則是擁抱風險 11/26 07:32
推 namkk : 所以才有“風險效率前緣” 11/26 07:34
→ namkk : 透過多資產配置 11/26 07:34
→ namkk : 每一份風險才能換到最大報酬 11/26 07:34
→ afflic : 效率前緣其實跟夏普比率有一樣的問題 11/26 07:37
→ afflic : 很多時候其實是因為波動很小而不是報酬很大 11/26 07:37
推 spike1215 : 還是不太理解,這樣的話拿正二和反一去再平衡不就 11/26 07:37
→ spike1215 : 無敵? 11/26 07:37
→ afflic : 多空都做,方向對的話的確是無敵啊 11/26 07:37
→ sheenscott : 必須要說的是,風險(或者你要說波動率,還是價格 11/26 07:38
→ sheenscott : 標準差也好,同一個東西)大的東西,不一定代表報 11/26 07:38
→ sheenscott : 酬率更好,所以為什麼sharpe ratio在大多數的資產 11/26 07:38
→ sheenscott : 組合裡面,還是一個不錯的評估工具的原因 11/26 07:38
→ sheenscott : 不過有報酬,不管波動率好不好就直接衝上去,那我 11/26 07:38
→ sheenscott : 覺得這不是在投資,比較像是賭博 11/26 07:38
→ sheenscott : 實際上可以透過合理的資產配置,設定比例跟槓桿率 11/26 07:38
→ sheenscott : ,來達成接近甚至超過all-in正2的報酬,那為什麼不 11/26 07:38
→ sheenscott : 去研究? 11/26 07:38
→ sheenscott : 因為困難所以不去想、找方法,挑一個簡單但是已經 11/26 07:38
→ sheenscott : 被證明風險的策略抱著,我覺得不是一個投資人該有 11/26 07:38
→ sheenscott : 的心態 11/26 07:38
→ sheenscott : 正2是個很好的工具,拿來放在資產組合調整並且減少 11/26 07:38
→ sheenscott : 自己的操作壓力,但是all-in然後buy-and-hold,我 11/26 07:38
→ sheenscott : 覺得要再想想 11/26 07:38
→ afflic : 但台指期是長期向上的,用現金的效果可能比反一好 11/26 07:38
→ afflic : 要不要歐印的確要看每個人的投資習慣 11/26 07:40
→ afflic : 至於正二本來就不是一個完美的工具 11/26 07:40
→ afflic : 自己用台指期做成本更低 11/26 07:40
→ afflic : 正二只是一個比較方便而且可以解決人性的工具而已 11/26 07:40
→ sheenscott : spkie大,槓桿型ETF本身因為有波動率扣血(然後反1 11/26 07:41
→ sheenscott : 扣的比正2痛,有公式可以證明),所以本質上是在「 11/26 07:41
→ sheenscott : 做空」波動率 11/26 07:41
→ sheenscott : 如果你是想討論我提到的那個shannon's demon的話, 11/26 07:41
→ sheenscott : 是有一套方法,不過不是用做多ETF來達成的:) 11/26 07:41
推 Gipmydanger : 你抱原型指數還不是一樣? 11/26 07:43
推 linclan : 推,用統計手法解釋了我長久以來的疑問 11/26 07:43
→ afflic : 至於波動率跟報酬率的比較 11/26 07:45
→ afflic : 建議可以看看實際市場上賺錢的標的 11/26 07:45
→ afflic : 他們的波動率跟報酬率分別都是怎樣 11/26 07:45
→ afflic : 大概就可以理解我說的了 11/26 07:45
→ afflic : 你要說是賭博嗎? 我不能否認 11/26 07:45
→ afflic : 但你要說不是投資嗎? 如果能長期向上就是投資吧 11/26 07:45
→ Gipmydanger : 資產配置本來就是基本,留一半現金也不只是歪打正 11/26 07:46
→ Gipmydanger : 著。表示你沒有遇過現實中的問題而已。保險買越多 11/26 07:46
→ Gipmydanger : 期望值負越多難道就不要買保險嗎? 11/26 07:46
推 ben121196 : 自己是正三黃金再平衡 黃金跟股票相關很低 又不像現 11/26 07:47
→ ben121196 : 金被通膨吃 11/26 07:47
推 namkk : 股票 債券 房地產 我全都要 11/26 07:48
→ sheenscott : well,我這邊歪打正著的意思,其實是指在沒有用數學 11/26 07:49
→ sheenscott : 來思考的情況下,得出了類似的結果的意思 11/26 07:49
→ sheenscott : 順帶一提,保險其實也可以用統計學來看,只是他是 11/26 07:49
→ sheenscott : 在分析一個負偏的事件:) 11/26 07:49
→ afflic : 今年四月大概就是那種左尾極端分布的時候吧 11/26 07:49
→ afflic : 但四月如果敢進場,抱到現在都賺翻了 11/26 07:49
→ afflic : 你說這是賭博還是投資呢 11/26 07:49
→ sheenscott : 我不會認為那個叫「敢進場」,從資產組合的角度來 11/26 07:52
→ sheenscott : 看,那個下跌的時間點本來就是各類資產再平衡的時 11/26 07:52
→ sheenscott : 機,所以我才會強調是從「總體資產組合」規劃的角 11/26 07:52
→ sheenscott : 度出發 11/26 07:52
→ sheenscott : 邏輯上還是跟指數派共用底層邏輯,我不離開市場, 11/26 07:52
→ sheenscott : 長期參與市場,但是想辦法運用數學,尋求一個最大 11/26 07:52
→ sheenscott : 化報酬,盡可能降低風險或是MDD的策略 11/26 07:52
→ sheenscott : 另外,用個股的波動與報酬跟大盤相關的指數來看, 11/26 07:55
→ sheenscott : 我覺得稍微沒那麼有可比性 11/26 07:55
→ sheenscott : 從因子的角度來看,大盤本來就是把所有因子給平衡 11/26 07:55
→ sheenscott : 掉,只留下那個最純的beta,我們是利用數學的方式 11/26 07:55
→ sheenscott : 來組合出勝率更高的選擇 11/26 07:55
→ sheenscott : 個股不一樣,本身就充滿著各種因子在自己身上,波 11/26 07:55
→ sheenscott : 動性跟報酬性都可能很大 11/26 07:55
→ sheenscott : 我自認不是基本面高手,所以我選擇從自己比較熟悉 11/26 07:55
→ sheenscott : 的數學來切入指數投資而已 11/26 07:55
推 mimchu : 好文 11/26 07:55
推 kami0857 : 謝謝分析 11/26 07:55
推 SSCSFE : 跌破200MA就清掉的依據印象中是原形在200MA以下的 11/26 07:56
→ SSCSFE : volatility會比200MA以上還大 考慮LEFT本身有 11/26 07:57
推 yannicklatte: 推 11/26 07:57
→ SSCSFE : volatility drag 所以要避掉那個區間 11/26 07:57
推 askaa : Gi有一句話講得很對 年輕人最大的優勢就是時間 11/26 07:58
→ askaa : 年輕就算破產也沒差可以一直試錯 11/26 07:58
→ askaa : 然後努力又有認知的 抓到風口就上天了 11/26 07:59
→ lalacos123 : A大別糾結了 這些本來就是講給不敢跳下水的人評估 11/26 08:00
→ lalacos123 : 的 有自己的定調敢吃兩倍回調的人 在考慮的不會是這 11/26 08:00
→ lalacos123 : 些 11/26 08:00
→ lalacos123 : 推 這兩篇給想跳進來的人含金量很高 11/26 08:01
推 fisher6879 : 推 11/26 08:02
→ sheenscott : 竊以為如果真的有這種敢賭破產的衝勁,應該去拼創 11/26 08:03
→ sheenscott : 業而不是在證券市場就是了XD 11/26 08:03
→ sheenscott : 畢竟自己的親身體驗,雖然風險高,但是帶來的報酬 11/26 08:03
→ sheenscott : 也是遠高於證券市場,如果真的想賭一把的話 11/26 08:03
→ afflic : 是蠻好奇風險趨避的人看完會比較敢投嗎 11/26 08:03
→ afflic : 創業的難度跟投資比起來難多囉…… 11/26 08:04
推 zpf2005 : 感謝,收獲良多。大仁哥文章提到,正2最後的獲利看 11/26 08:05
→ zpf2005 : 重原型ETF的報酬率跟波動率,不是每個指數ETF都能無 11/26 08:05
→ zpf2005 : 腦正2,當然ETF過去的報酬只能參考不等於未來的獲利 11/26 08:05
→ zpf2005 : ,這是使用正2前該有的認知 11/26 08:05
→ zpf2005 : 人在投資的時侯其實很難歐印,要養的人越多要預留的 11/26 08:05
→ zpf2005 : 準備金就越多,用50/50保持曝險100%,現金部分來取 11/26 08:05
→ zpf2005 : 代緊急準備金,我覺得是勝過高股息ETF跟歐印原型ETF 11/26 08:05
→ sheenscott : 我原意其實是希望澄清一下正2風險,然後重新用數學 11/26 08:05
→ sheenscott : 的角度出發來解釋50/50再平衡的優勢 11/26 08:05
→ sheenscott : 看能不能結合第一篇的最適槓桿率來給出一些啟發啦 11/26 08:05
→ sheenscott : 不過感覺好像越繞越遠了 (笑 11/26 08:05
推 Gipmydanger : 再鑽牛角尖下去就會變成多啦王一樣,配置各種五花 11/26 08:09
→ Gipmydanger : 八門,取得不痛不癢的低風險報酬 11/26 08:09
→ askaa : 在投資這條路上其實一直都是不只一個重點 11/26 08:09
→ askaa : 所以討論來討論去 歪掉超級正常 顆顆 11/26 08:10
→ Gipmydanger : 這就是嘗試用數學弭平波動,最後的歸途 11/26 08:10
推 Lii4 : 先推 11/26 08:11
→ Lii4 : 不過最適槓桿率那邊看起來是用二元樹去算的 11/26 08:11
→ Lii4 : 直接用隨機漫步去算答案會多個 1/2 11/26 08:11
→ Lii4 : 所以我認為很多人都低估了槓桿率 11/26 08:11
→ Lii4 : 我個人是打算放30年以上啦 11/26 08:11
→ Lii4 : 所以就直接把標準差這個東西當作沒看到了 11/26 08:11
→ askaa : 我也有朋友是偽多拉王 每次挑股很準 結果都只買一張 11/26 08:12
→ afflic : 其實說到後來結論應該還是沒變吧 11/26 08:12
→ askaa : 問他為啥部大筆直接砸下去?結果其實都是老問題 11/26 08:12
→ afflic : 歐印沒意外應該是報酬最高的方式 11/26 08:12
→ afflic : 但要克服人性弱點跟左尾風險的問題 11/26 08:12
→ afflic : 50/50再平衡很可能不會報酬最高但可以克服上述缺點 11/26 08:12
推 wayne5347 : 認真文 必推 11/26 08:12
→ afflic : 如果想深入了解其中的數學邏輯再去仔細研讀了 11/26 08:12
→ askaa : 後來我就理解 其實就是大仁說的老話 11/26 08:13
→ askaa : "你有多少認知 就決定了你有多少報酬" 11/26 08:13
→ lalacos123 : 哈 這篇就是在講 不要斷定一定會走出最好的那條路徑 11/26 08:14
→ lalacos123 : 啊XD 11/26 08:14
→ askaa : 講得很厲害 但是一毛都不敢下 你就知道這人的水平了 11/26 08:14
推 dreamdds : 反正都是在找比歐印大盤風險更低報酬更高的解法而已 11/26 08:14
→ afflic : 這個世界上本來就沒有一定就是了 11/26 08:15
→ afflic : 只能說歷史數據上看來是這樣 11/26 08:15
→ lalacos123 : 只是你可以用一些方法 如再平衡 或動態調整槓桿 讓 11/26 08:15
→ lalacos123 : 自己不要變成最差的那條路 11/26 08:15
推 Gipmydanger : 回歸到能承受的曝險,適度就好,不要太鑽牛角尖, 11/26 08:15
→ Gipmydanger : 找到數學上的聖盃最佳化投資姿勢跟角度,你照樣會 11/26 08:15
→ Gipmydanger : 遇到尾部風險。何必 11/26 08:15
→ afflic : 真的 做股票不能太悲觀 不然會一直砍在阿呆谷 11/26 08:16
→ lalacos123 : 的確 膽小的人就多閃一點 少賺一點 能扛的就想閃就 11/26 08:17
→ lalacos123 : 閃 不想就算 11/26 08:17
→ Gipmydanger : 難道你上班開車會全副武裝戴安全帽改防撞籠嗎?包 11/26 08:17
→ Gipmydanger : 包拎了就上啦 11/26 08:17
→ afflic : 當然 也有可能明天就發生黑天鵝事件 11/26 08:18
→ afflic : 讓你所有資產一夕歸零 11/26 08:18
→ afflic : 但如果擔憂太多就變成杞人憂天了 11/26 08:18
推 l14567p : 好文 謝謝分享 11/26 08:19
→ afflic : 台股已經算長期向上表現不錯的市場了 11/26 08:19
推 ben2227486 : 好文 解決我很多再跑回測制定策略時產生的疑問 原來 11/26 08:23
→ ben2227486 : 我這麼才疏學淺 只是歪倒正著QQ 11/26 08:23
推 easonshih99 : 先叫小胡起床追漲停了 11/26 08:30
推 Gipmydanger : 這算是一種數學潔癖嗎? 11/26 08:30
推 awss1971 : 1. 長期"預期報酬"是原型1.4倍 11/26 08:32
→ awss1971 : 2. "日波動"是原型2倍 11/26 08:32
→ awss1971 : 3. 1&2,nji3u3 11/26 08:32
推 no2muta : 好文推 11/26 08:33
→ ffaarr : 台股近10年不是「表現不錯」而已,是強到全世界第一 11/26 08:34
→ ffaarr : 而且是沒對手在同個水準的第一。 11/26 08:34
推 awss1971 : 1. 長期"預期報酬"是原型1.4倍 11/26 08:34
→ awss1971 : 2. "日波動"是原型2倍 11/26 08:34
→ awss1971 : 3. 報酬具有"強烈"路徑依賴 11/26 08:34
→ awss1971 : 4. 沒人可以預測未來長期走勢 11/26 08:34
→ awss1971 : 5. 我心臟小,所以只有不到10%放正二(QLD) 11/26 08:34
→ sheenscott : 沒想到可以引來哆啦王推文,獻醜了QQ 11/26 08:35
→ afflic : 悲觀的人會跟你說均值回歸 11/26 08:35
→ afflic : 未來台股沒人知道會不會持續強下去 11/26 08:35
→ ffaarr : 所以正二特別強很正常。 11/26 08:35
→ ffaarr : 然後推一下這篇好文 11/26 08:35
→ afflic : 是說有強到世界第一嗎?? 11/26 08:36
推 sh910715 : 正二有路徑相依的風險 11/26 08:36
推 ben2227486 : 對一般人來說確實也不用關注過程的波動風險 只要知 11/26 08:36
→ ben2227486 : 道最後預期報酬約是13.5% vs 9.1% 衰小的情況大概會 11/26 08:36
→ ben2227486 : 年化0.7% vs 3.9% 機率還不低 但是可以透過再平衡策 11/26 08:36
→ ben2227486 : 略主動抹平這種風險 這樣就夠了 11/26 08:36
→ afflic : 有人可以白話解釋一下路徑相依嗎 11/26 08:37
→ ffaarr : 台股msci指數10年化超過18%,已很強的美股才14% 11/26 08:38
→ ffaarr : 第二名的捷克17% 11/26 08:38
→ ffaarr : 10年差1%總報酬就差一截了 11/26 08:38
→ sheenscott : 樓上想聽excel乘法版,還是隨機分析的推導版(x 11/26 08:38
推 Gipmydanger : 就是你從台中到台北,最後都是會到台北。但是你有 11/26 08:40
→ Gipmydanger : 千萬種路可以走,你選擇走不同的路,最後一下車發 11/26 08:40
→ Gipmydanger : 現錢包裡面的錢完全不一樣多。 11/26 08:40
→ afflic : 聽起來所有標的都有這個問題 11/26 08:41
→ ffaarr : 這裡是拿49個已開發和新興市場來排名。 11/26 08:41
→ ffaarr : 很多標的都沒有路徑的問題啊。 11/26 08:41
→ ffaarr : 原型ETF,指數超點終點在哪 就拿到接近報酬 11/26 08:42
→ afflic : 什麼標的沒有路徑的問題? 11/26 08:42
推 voyager520 : 哇 這是我要的股版! 11/26 08:42
→ Gipmydanger : 於是你越想越鑽牛角尖下去,你就就不會配置零零五 11/26 08:42
→ Gipmydanger : 零改配置美國,然後再改成配置全世界,然後再改成 11/26 08:42
→ Gipmydanger : 配置股債配,然後再改成配置各種五花八門的資產什 11/26 08:42
→ Gipmydanger : 麼貴金屬房地產原物料亂七八糟的 11/26 08:42
→ sheenscott : 是,所以才會說市場其實不是常態分布 11/26 08:42
→ sheenscott : 但是槓桿的偏度會更嚴重,然後LETF這種每日再平衡 11/26 08:42
→ sheenscott : 的會直接相依到要單獨拉出來做別的數學分析 11/26 08:42
→ Gipmydanger : 因為他是比較的基準,所以當然看起來沒這種問題呀 11/26 08:43
→ Gipmydanger : 你會說這個東西是1公尺長,那是因為你拿1公尺去比 11/26 08:43
→ Gipmydanger : 較 11/26 08:43
→ afflic : 美股14%是用標普500算的嗎? 11/26 08:43
→ ffaarr : 然後實務上很多原型4%以下的,正二ETF都變負報酬。 11/26 08:43
→ ffaarr : msci imi index 11/26 08:44
→ sheenscott : 不過其實根據shannon's demon的概念,你把LETF當初 11/26 08:45
→ sheenscott : 配置的一環的時候,她自己是正報酬還是負報酬只是 11/26 08:45
→ sheenscott : 影響在你算權重的時候而已 11/26 08:45
→ sheenscott : 不過再講下去就真的完全進入量化的領域了,超過這 11/26 08:45
→ sheenscott : 篇文想討論的主題了w 11/26 08:45
推 gboyQQ : 清流 11/26 08:50
推 suja : 對 我也是這麼想 11/26 08:51
推 metallolly : 先推~免得大家發現我看不懂 11/26 08:56
推 Gipmydanger : 你把比較的基準改為0.5倍指數,0.87倍指數,再去比 11/26 08:56
→ Gipmydanger : 其他1倍2倍蝦78倍,全部都有路徑依賴問題 11/26 08:56
推 Gipmydanger : 所以路徑依賴不是什麼問題,你上班賺多少錢,你有 11/26 08:58
→ Gipmydanger : 多少抗風險能力才是問題 11/26 08:58
推 awss1971 : 任何標的都有路徑依賴(O) 11/26 08:59
→ awss1971 : 但原PO強調的是: 槓桿相對原型有更強烈的路經依賴性 11/26 08:59
推 Gipmydanger : 所以賺錢不要想的太難,你不是大神量化基金 11/26 09:01
推 Gipmydanger : 追求極致的平庸應該不是一般人想要的 11/26 09:02
→ Gipmydanger : 那是吉良吉影的生活目標 11/26 09:02
推 zerg999 : 大仁有一篇提到市場原型報酬>8%以上才適合正二 11/26 09:03
→ zerg999 : 並非所有市場都適合,剛好台灣符合 11/26 09:04
→ Gipmydanger : 你如果沒什麼錢又一接觸市場就VT幹到底的話,那你 11/26 09:13
→ Gipmydanger : 老了的時候風險就跟灰犀牛一樣一定會到 11/26 09:13
推 Gipmydanger : 這邊的風險叫做活太久,錢不夠用。不是什麼波動率 11/26 09:18
推 thinktwice31: 謝謝分享,很詳細的說明 11/26 09:20
推 rex0707 : 認真分析推 11/26 09:20
推 epion : 好文,值得細細研讀! 11/26 09:21
推 smallstudent: 推 11/26 09:24
→ chi7499 : 有沒有結論啊 太長了。到底能不能買 11/26 09:32
推 Gipmydanger : 你不了解產品買回來你也賺不了錢,就這麼簡單。 11/26 09:33
推 hihi29 : 正二教要沒落了嗎 不~~~~~~~ 11/26 09:34
推 clisan : 推 11/26 09:37
推 BleuSaphir : 感謝分享 11/26 09:37
推 Destiny6 : 感謝分享 11/26 09:40
推 umidaisuki : 謝謝分享 11/26 09:41
推 hsupaijay : 推個,打臉教徒惹 11/26 09:43
→ lalacos123 : 靠杯 樓上這結論XD 11/26 09:48
推 repast : 推優質好文 謝謝分享! 11/26 09:53
推 onekoni : 正二王 11/26 09:56
推 veniesbetty : 推分析,謝謝分享 11/26 09:57
推 zzz50126 : 這篇文太強了 必須要說正2真的沒有這麼好 拿台灣回 11/26 10:07
→ zzz50126 : 測的更是有問題 但我還是會買 11/26 10:07
推 linyellow : 所以用可以用期貨來取代正二會比較好嗎? 11/26 10:07
推 jjj85811s : 推 11/26 10:07
推 Ericfox : 推 11/26 10:09
推 ben2227486 : 期貨的問題大仁哥講解得不錯 你能突破人性弱點那他 11/26 10:16
→ ben2227486 : 就是比槓桿ETF更好的工具 反之則否 11/26 10:16
噓 davis0918 : 正二問題是大盤正二 不是純50正二 太多雜魚 11/26 10:20
推 ups : 佛 11/26 10:21
推 rebel : 推認真分析文 11/26 10:24
推 witows : 推 11/26 10:26
推 zxcvbnm6102 : 推分析 11/26 10:29
推 rebel : 順便請教原po一個也是困擾我很久的正二問題 看你知 11/26 10:37
→ rebel : 不知道答案 很多人說單日兩倍平衡沒必要 那有沒有 11/26 10:37
→ rebel : 多久平衡一次是比較好的數據?我知道這一定有路徑 11/26 10:37
→ rebel : 相依 但應該回測會有一個勝率比較高的區間? 11/26 10:37
推 s887540 : 推,謝謝分析! 11/26 10:39
推 biojo : 好棒 更了解正二優缺點 值得m 11/26 10:40
推 YuSeaFood : 好文 11/26 10:41
推 nthukos : 先推再看 11/26 10:51
推 nthukos : 好像應該多推幾次的 11/26 10:56
推 johnsonhoj : 謝謝分享 11/26 11:01
推 toddy5401 : 好文章 值得推薦 11/26 11:02
推 daniel74327 : 感謝分享 還是買指數比較不費心 11/26 11:03
推 windfeather : 推分享 11/26 11:05
推 jayys5048aam: 認真推 11/26 11:12
推 kyukyu : push 11/26 11:26
推 kyukyu : push 11/26 11:33
推 st264201 : 推! 正二哥在社團有回覆您了 有機會看到您針對他的 11/26 11:38
→ st264201 : 回覆再做說明嗎 感謝 11/26 11:38
推 CIIIO : 股版難得優文 偷酸薪資都在右尾XD 11/26 11:41
推 leo761212 : 想知道大大說的透過資產配置來達到正二的報酬率甚 11/26 11:44
→ leo761212 : 至超過,請問有哪些書或是資料能研究呢?感謝!! 11/26 11:44
→ Watanabe : 大仁哥社團回應了 11/26 11:47
推 dophin332 : 言之有物 11/26 11:52
→ w901741 : 好奇 在分析正二路經的時候應該沒有加上熔斷機制, 11/26 12:02
→ w901741 : 台灣正二 一天最多就跌20%,這個機制會導致台灣的 11/26 12:02
→ w901741 : 正二報酬率更好 11/26 12:02
推 winken2004 : 推 11/26 12:14
推 as5566321 : 讚 11/26 12:22
推 toby4848 : 推,認真 11/26 12:23
推 pinwei0989 : 難得好文 大仁哥也回覆了~ 11/26 12:25
→ icedog122 : 推 11/26 12:28
推 winken2004 : 推 11/26 12:39
推 rebel : 感謝回覆再平衡頻率問題 主要是想說 萬一未來想自 11/26 12:42
→ rebel : 己操作期貨達成正二效果 叫我每日平衡一定不幹 寧 11/26 12:42
→ rebel : 願付個0.5/0.6%給ETF去弄 但如果是一周或雙周再平 11/26 12:42
→ rebel : 衡 自己弄還可以考慮 11/26 12:42
推 Dusha : 推 11/26 12:53
→ ctx705f : 熔斷可以防止超過20% 但今年川普拳的問題就是券商沒 11/26 13:17
→ ctx705f : 辦法把曝險調整回200% 印象中當時曝險超過200% 11/26 13:17
推 pindar : 有人知道大仁哥推的line群在做啥? 11/26 13:20
→ ctx705f : 大仁沒有賴群 11/26 13:26
推 onekoni : 再平衡有利在連漲連跌 台股2016後走勢都是這樣 11/26 13:27
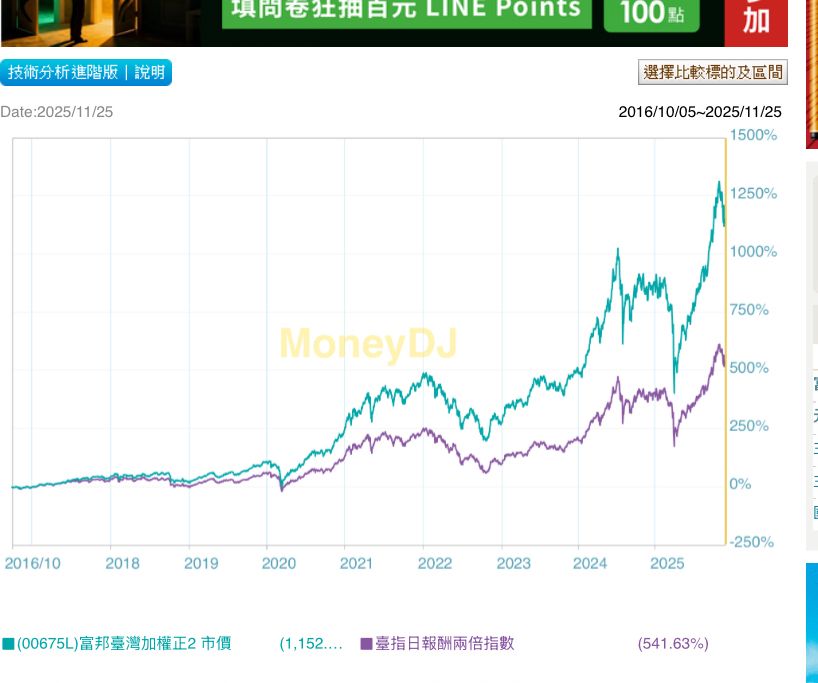
→ onekoni : 所以才贏報酬指數兩倍那麼多 11/26 13:28
→ onekoni : 至於為什麼 跟美中貿易戰後帶來的轉型有關 11/26 13:29
推 SmilD : 感謝分享 11/26 13:36
推 n64tw : 推好文,可以直接顯示圖就更好了 11/26 13:36
推 Gipmydanger : 詐騙才有line群 11/26 13:40
推 pyroru : 推 11/26 13:41
推 BruceChen227: 推 11/26 13:50
推 babosa633 : 推 11/26 13:56
→ biojo : 大仁哥社團有很多詐騙分身 不要被騙 11/26 13:57
推 Kenneth10 : 推 11/26 14:01
推 molopo : 推 11/26 14:05
推 aa00788 : 推個 狠狠打臉正二派 療癒 11/26 14:35
推 dickygto : 先說我不是信仰正2神教的人,但我覺得你跟大仁哥滿 11/26 15:56
→ dickygto : 像的,只是想法不同,顆顆,果然還是要魔法對決魔 11/26 15:56
→ dickygto : 法 11/26 15:56
→ Gundam77 : 窮人核彈輸沒多少,不至於裸奔但縮短到達標的的時間 11/26 16:06
→ ookimoo : 12月再拉一次上去,沒跑的人會套一輩子 11/26 16:20
推 gelegelego : 好屌 11/26 18:29
推 f204137 : 字好多 所以我只放20萬在正2 湊湊熱鬧哈 11/26 19:03
推 RedLover1009: 這篇受益很多,收藏起來 11/26 21:54
推 yoyoleader : 感謝大大用心分享,文章已收藏 11/26 22:00
推 johnsonhoj : 謝謝分享 11/27 07:20
→ ShiuanRefuel: 差距這麼大竟然還有人說和大仁很像@@ 11/27 08:04
推 Lhmstu : 老實講3萬瓢路線是沒有任何意外的情況下,現在就是 11/27 09:27
→ Lhmstu : 在AI拐點上,這算法沒考慮到時代拐點 11/27 09:27
推 abc0922001 : 好文章 11/27 10:16
推 luke1130 : 優質好文 11/27 12:38
→ luke1130 : 正二是好工具沒錯 11/27 12:38
→ luke1130 : 但不是像大盤原型能無腦all in 11/27 12:38
推 abc32521 : 推 認真分析的好文章 11/27 14:51
推 staytuned74 : you are correct on math try Letf/etf 11/27 14:56
推 staytuned74 : monte carlo , you can see the tail risk 11/27 15:00
→ staytuned74 : "it's really time period dependent" 11/27 15:02
→ staytuned74 : maybe focus on sortino, not sharpe, imo 11/27 15:04
推 gary886 : 解釋了很多我對正2的疑惑,謝謝分享 11/27 15:33
推 vendee : 這真是專業 11/27 21:30